Banking Supervision

Regulators and central banks often need large amounts of networked data to understand the intricate links between entities that on surface may seem independent of each other.

Company Control

Company control is a staple in the analysis of ownership structures, and is concerned with decision power, i.e., whether a company can direct the decisions of another company by controling the majority of its shares.

To determine whether a company X controls a company Y, we consider two rules:

1. X directly owns more than 50% of Y; or,
2. X controls a set of companies that jointly, and possibly together with X itself, own more than 50% of Y.

This problem can be modeled via the following set of recursive Vadalog rules.

% base case: if a company X owns Y with shares Q then there is direct a
% controlled_share relationship from X to Y with share Q
controlled_shares(X,Y,Y,Q) :- own(X,Y,Q), X<>Y.

% recursive case: if a company X controls Y with shares K
% and the company Y owns Z with share Q, then there there is a indirect
% controlled_share relationship from X to Y via Z with share Q
controlled_shares(X,Z,Y,Q) :- control(X,Y), own(Y,Z,Q), X<>Z, Z<>Y, X<>Y.

% if X has controlled_shares of Y, via any company Z with shares Q, then the total
% controlled share are computed with an aggregation msum, that groups
% by X and Z and aggregates the sum of Q
total_controlled_shares(X,Y,S) :- controlled_shares(X,Y,Z,Q), S=msum(Q).

% if the total controlled shares Q of Y by X is greater than 0.5, then X
% control Y with shares Q.
control(X,Y) :- total_controlled_shares(X,Y,Q), Q>0.5.

@output("control").

Let's now consider this set of organisations:

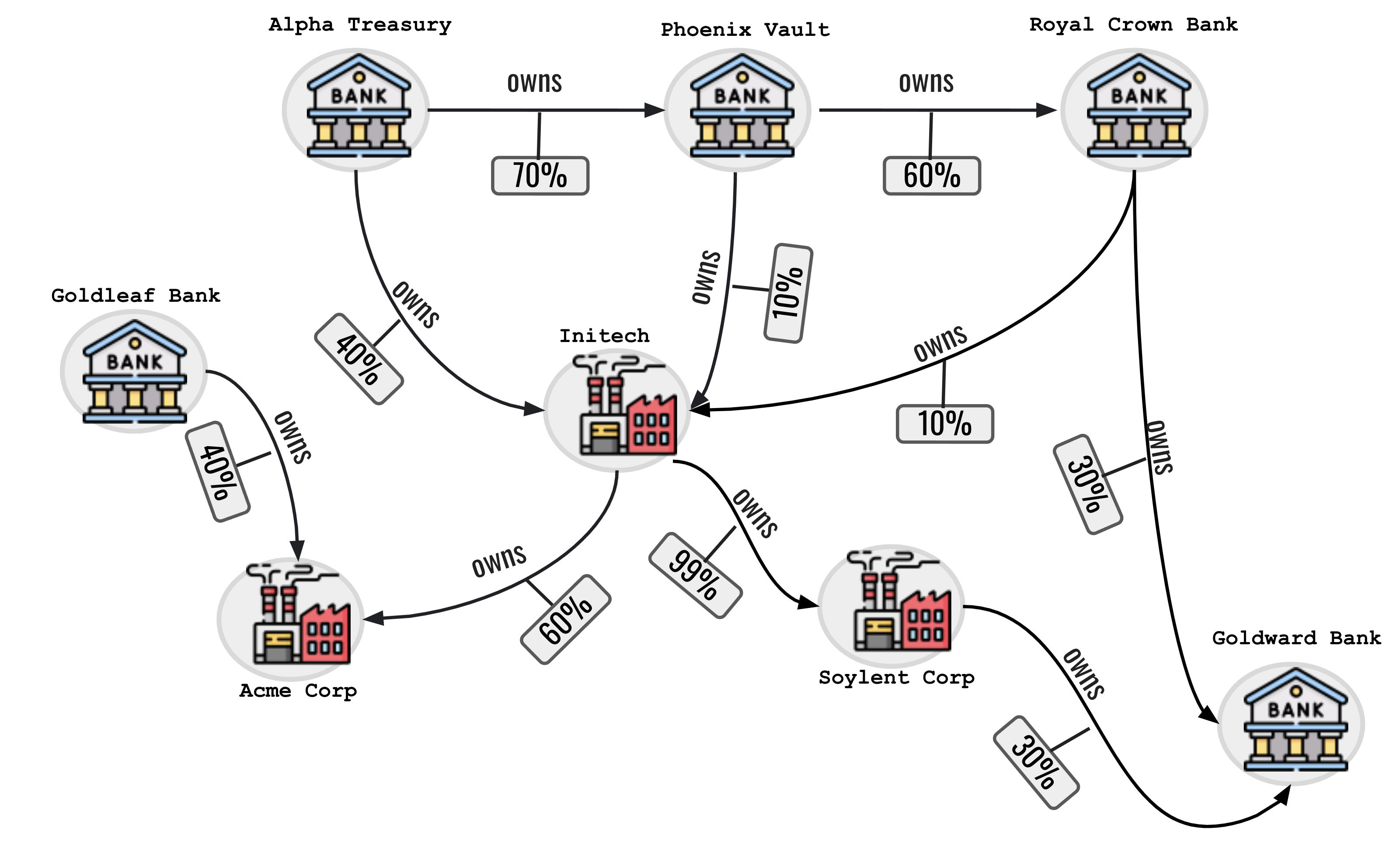
We can model the above graph using the following set of input facts:

own("Alpha Treasury","Phoenix Vault",0.7).
own("Alpha Treasury","Initech",0.4).
own("Phoenix Vault","Initech",0.1).
own("Phoenix Vault","Royal Crown Bank",0.6).
own("Royal Crown Bank","Initech",0.1).
own("Royal Crown Bank","Goldward Bank",0.3).
own("Goldleaf Bank","Acme Corp",0.4).
own("Initech","Acme Corp",0.4).
own("Initech","Soylent Corp",0.99).
own("Soylent Corp","Goldward Bank",0.3).

After reasoning, we can see the "Alpha Treasury" indirectly controls many of the other institutions, including "Godward Bank", via a long chain of control.

control("Alpha Treasury","Phoenix Vault").
control("Alpha Treasury","Royal Crown Bank").
control("Alpha Treasury","Initech").
control("Alpha Treasury","Soylent Corp").
control("Alpha Treasury","Godward Bank").
control("Phoenix Vault","Royal Crown Bank").
control("Initech","Soylent Corp").
control("Initech","Acme Corp").

---

Close Link Detection

This scenario consists in determining whether there exists a (direct or indirect) link between two companies, based on a high overlap of shares.

Formally, two companies 𝑐1 and 𝑐2 are close links if X (resp. Y) owns directly or indirectly, through one or more other companies, 20% or more of the share of Y (resp. X).

Determining whether two companies are closely-linked is extremely important for banking supervision since a company cannot act as a guarantor for loans to another company if they share such a relationship.

% input company graph, described as ownerships edges
% the company A own 0.2% of shares of the comapany B
own("A", "B", 0.2).
% the company B own 0.8% of shares of the comapany A
own("B", "A", 0.8).
own("B", "C", 0.2).
own("C", "D", 0.6).
own("D", "A", 0.9).
own("A", "C", 0.2).

% if there the company X owns a percentage W of shares of Y and we add in a set
% the visited node X and the visited node Y, then there is a closeLinkPaths of X
% over Y with shares W and we bring the list of visited nodes P. We bring in the
% head the list and we will use it in recursive rule
closeLinkPaths(X,Y,W,P) :- own(X,Y,W), P={}|X|Y, X<>Y.

% if there is a closeLinkPath from X to Y with shares W1 with a set of visited
% nodes P1, and the node Z is not in the list of the visited nodes, the node Z is
% added in the set of visited nodes, then there is a closeLinkPaths from X,Z
% with visited nodes P
closeLinkPaths(X,Z,J,P) :- closeLinkPaths(X,Y,W1,P1),
                           own(Y,Z,W2),
                           J = W1\*W2,
                           P = P1|Z,
                           Z !in P1.

% if there is a closeLinkPaths from the company X to the company Y with shares W
% and the set of visited nodes P, then there is a close_link_sum by grouping by
% X and Y with totale share J, by aggregating the sum of W
close_link_sum(X,Y,J) :- closeLinkPaths(X,Y,W,P), J = msum(W).

% if there is a close_link_sum of X over Y with shares W, and the shares is
% greater than 0.2, then the companies X and Y are in close link with shares W
close_link(X,Y,W) :- close_link_sum(X,Y,W), W >= 0.2.
@output("close_link").

After execution, the relation close_link contains the following tuples:

% Output of close_link(X,Y,W)
close_link(A, C, 0.24).
close_link(B, D, 0.216).
close_link(D, C, 0.216).
close_link(B, A, 0.908).
close_link(C, D, 0.6).
close_link(A, B, 0.2).
close_link(B, C, 0.36).
close_link(C, A, 0.54).
close_link(D, A, 0.9).