Recursion

Recursion is the workhorse of Prometheux, and is a pattern that occurs naturally in many situations. In all recursive cases, there is :

1. a recursive case, where a predicate is derived by itself, and
2. a base case, which must not be derivable by itself, allowing the recursion to terminate.

Consider a graph of nodes and edges between them. A path can be defined as:

1. A simple edge between 2 nodes.
2. The list of such edges between any 2 nodes, via N-2 other nodes.

path(Start, End) :- edge(Start, End). % Base case
path(Start, End) :- path(Start, Via), edge(Via, End). % Recursive case

See how path can be a simple hop from one node to another, or requires 2 hops (via 1 intermediate node), or via 3 hops (via 2 intermediate nodes).

Transitive Closure

The task of finding out all pairs of nodes in a graph that are connected to each other either directly or indirectly is known as transitive closure. You might think of this asking if it's possible to fly from some airport to another in one or more direct flights.

Consider the following small graph:

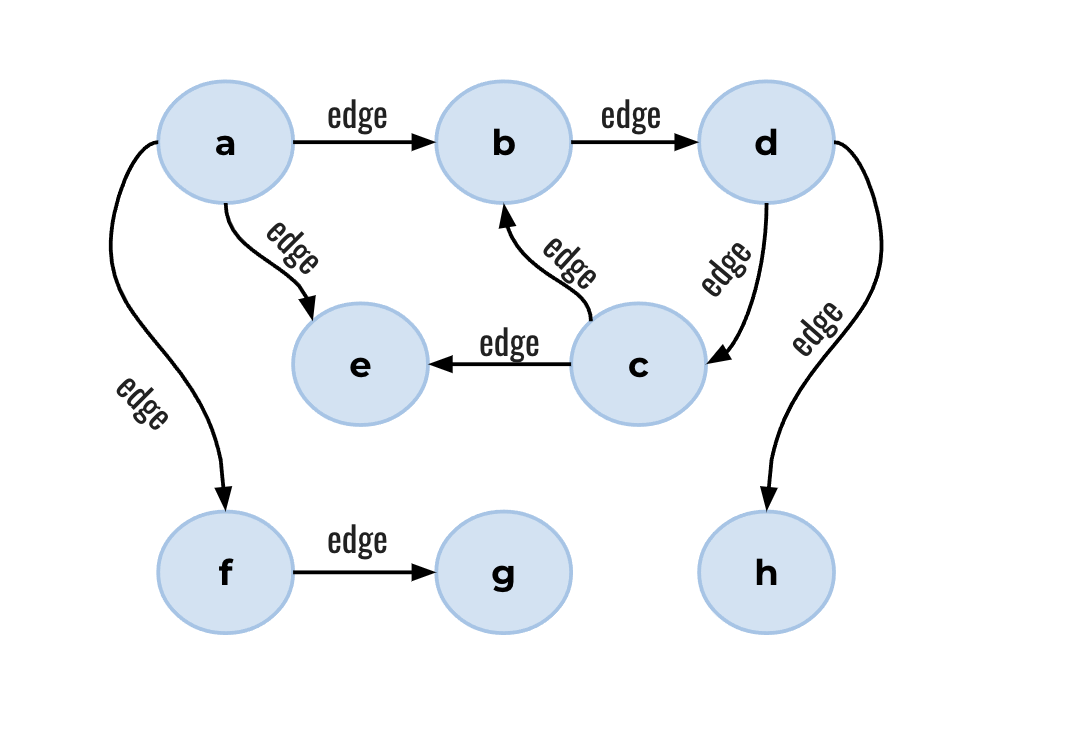
edge("a","b").
edge("a","e").
edge("a","f").
edge("b","d").
edge("c","b").
edge("c","e").
edge("d","c").
edge("d","h").
edge("f","g").

% base case: if there is and edge from the node X to the node Y then there is a path from X to Y %
path(X,Y) :- edge(X,Y).

% recursive case: if there is a path from the node X to the node Y and there is an edge from the node Y to the node Z, then there is a path from the node X to the node Z %
path(X,Z) :- path(X,Y),edge(Y,Z).

@output("path").

After execution, the relation path contains the following tuples:

% Output of path(X,Z)
path("a","e").
path("b","d").
path("f","g").
path("c","b").
path("d","h").
path("a","b").
path("a","f").
path("c","e").
path("d","c").
path("c","d").
path("a","g").
path("d","b").
path("b","h").
path("b","c").
path("a","d").
path("d","e").
path("b","b").
path("c","c").
path("d","d").
path("a","c").
path("b","e").
path("c","h").
path("a","h").

From a, you can arrive at any other node. However, from b, you may only visit c,d,e and h.